백준 1520번 : 내리막 길

처음에는 최단거리이면서 내리막길을 구하는 것인줄 알고 쉽네?! 하면서 했서 틀렸다... ㅋㅋ 문제를 잘 읽도록 하자.

단순 DFS만 적용하면 타임아웃이 날게 뻔하기 때문에 DP를 이용해 기록해두면 된다.

 

일단 DFS로 설명하면 (0, 0)에서 (x, y)로 가는 경로의 수를 count(x, y)라고 하자. (x, y)로 올 수 있는 경로는 다음 4가지이다.

(x, y)로 갈 수 있는 장소

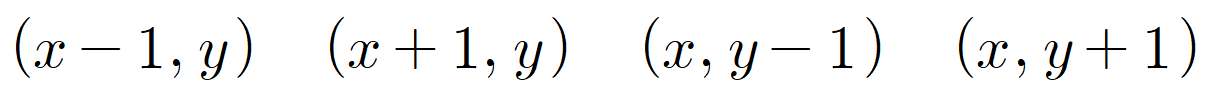
하지만 이 4 장소가 모두 유효한 장소는 아니다. 이들에 대해 2가지 조건이 붙는다.

1. 지도에 존재하는 장소일 것
2. (x, y)보다 값이 클 것 (같아서도 안된다!)

만약 위 두 조건을 모두 만족하는 위치가 (x - 1, y)와 (x, y + 1)이였다면 count(x ,y)는 다음과 같다.

순수 DFS로는 이렇게 되지만 매번 count함수를 통해 값을 구할 경우 구했던 장소를 또 구하고 또 구하는 불필요한 동작이 반복된다. 따라서 어딘가에 기록해두고 값이 있다면 가져와서 쓰고 없다면 count함수를 실행시키면 된다.

 

나는 cnt라는 2차원 배열에 기록을 해두었고 최초에 cnt 배열을 -1로 초기화해서 -1이면 값이 없다고 생각하고 그 좌표에 대한 count 함수를 실행했다.

 

#include <stdio.h>
#include <iostream>
 
using namespace std;

int n, m;
int dx[4] = { 1, -1, 0, 0 };
int dy[4] = { 0, 0, 1, -1 };
int arr[500][500];
int cnt[500][500];

int count(int x, int y)
{
    if(cnt[x][y] != -1) return cnt[x][y];
    
    cnt[x][y] = 0;
    for(int i = 0; i < 4; i++)
    {
        int nx = x + dx[i];
        int ny = y + dy[i];
        
        if(0 <= nx && nx < n && 0 <= ny && ny < m)
        {
            if(arr[x][y] < arr[nx][ny])
            {
                cnt[x][y] += count(nx, ny);
            }
        }        
    }
    
    return cnt[x][y];
}

int main()
{
    cin >> n >> m;
    
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < m; j++)
        {
            cin >> arr[i][j];
            cnt[i][j] = -1;
        }
    }
    
    cnt[0][0] = 1;
    
    cout << count(n - 1, m - 1);
 
    return 0;
}