백준 1256번 : 사전

  dp문제로 분류되어있긴 하지만 dp가 메인이 아니고 수열의 갯수를 구하기 위해서 사용되는 곁가지 느낌이었다. 이문제를 위한 기본적인 수학적 지식은 고등학교 경우의 수에서 배우는 '같은 것이 포함된 순열(Permutation)'이다.

 

a라는 문자 m개와 z라는 문자 n개로 만들 수 있는 문자열의 경우의 수

 

  각 문자는 최대 100개까지 존재할 수 있으니 dp는 이때 이 경우의 수를 저장하고 계산하는데 사용된다. 직접 팩토리얼을 재귀로 구현해서 구하면 당연하지만 시간초과가 발생한다.

  메인 로직은 하나하나 세나가는 것이 아니라 앞에서부터 문자를 확정시키면서 건너뛰어야 한다. a가 3개, z가 3개인 상황에서 예를 들어보면 다음과 같다.

 

 

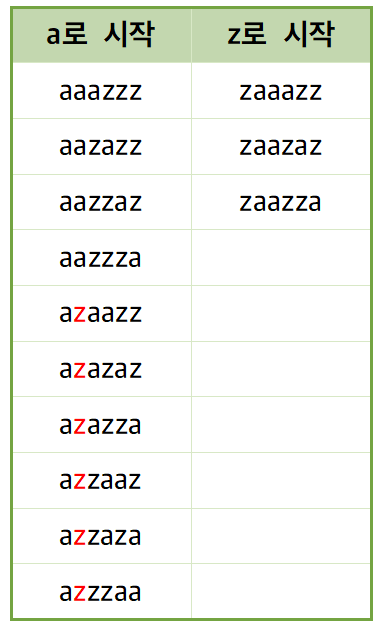
  n=3, m=3인 상황에서 k=6이라고 해보자. 첫번째 문자열이 a로 시작하는 문자열의 개수는 10개(=permu[2][3])이므로 문자열의 첫번째 자리는 a로 확정지을수 있다. 그 다음 두번째 문자열이 a로 시작하는 문자열의 개수는 4개(=permu[1][3])뿐이므로 두번째 자리는 z인 것을 알 수 있다. 두번째 자리를 z로 확정지으면서 두번째 자리가 a인 문자열의 개수만큼을 뛰어넘었으므로 k를 4(=두번째 자리가 a인 문자열의 개수)만큼 감소시킨다.

 

  위 알고리즘을 몇가지 경계조건을 넣어서 코드화 시키면 아래와 같다.

#include <iostream>
#include <string>

using namespace std;

int MAX = 1000000000 + 1;
int n, m, k;
int permu[102][102];
string ans;

int getPermu(int a, int b)
{
    if(permu[a][b] != 0) return permu[a][b];
    if(a == 0 || b == 0)
    {
        permu[a][b] = 1;
        return permu[a][b];
    }
    if(permu[b][a] != 0)
    {
        permu[a][b] = permu[b][a];
        return permu[a][b];
    }
    
    permu[a][b] = min(getPermu(a-1, b) + getPermu(a, b-1), MAX);
    
    return permu[a][b];
}

void word(int a, int z, int left)
{
    // 남은 a의 갯수가 0, 즉 z만 남은 경우 : 남은 z를 다 붙이고 종료
    if(a == 0)
    {
        for(int i = 0; i < z; i++) ans += 'z';
        return;
    }
    // 남은 z의 갯수가 0, 즉 a만 남은 경우 : 남은 a를 다 붙이고 종료
    if(z == 0)
    {
        for(int i = 0; i < a; i++) ans += 'a';
        return;
    }
    
    // a를 하나 제외한 수열의 경우의 수
    int flag = getPermu(a-1, z);
    
    if(left < flag)
    {
        ans += 'a';
        word(a-1, z, left);
    }
    else
    {
        ans += 'z';
        word(a, z-1, left - flag);
    }
}

int main()
{
    cin >> n >> m >> k;

    permu[0][0] = 1;

    if(getPermu(n, m) < k)
    {
        cout << -1;
        return 0;
    }

    word(n, m, k-1);
    
    cout << ans;

    return 0;
}